
- Date
- 14th January 2025
- Categories
- Clean Cooking
By Dr. Nigel Scott (Gamos Ltd.) and Prof. Matthew Leach (consultant to Gamos Ltd.).
Over the years the MECS programme has conducted or funded a number of cooking studies across many countries. For example, Cooking Diaries studies have generated detailed data on what people cook, when, how long it takes, and the amount of energy used. Recently, we reviewed these studies to extract data on the energy used to cook individual dishes when cooking with different fuels. Findings from an analysis of this reasonably large dataset (over 700 dishes cooked) were published in this peer-reviewed paper and include a few somewhat surprising findings.
I say surprising because received wisdom suggests that you can compare the amounts of any cooking fuel needed based on stove efficiency figures. The principle is said to be quite straight forward. The theory assumes that a certain amount of energy needs to be transferred to the pot in order to cook a dish, often referred to as the ‘useful energy’. The amount of fuel needed to deliver this useful energy then depends on the efficiency of the stove and fuel combination.
In this case the ‘useful’ energy, Eu, can be calculated as:
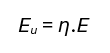
where η is thermal conversion efficiency, and E is gross fuel energy input. We can then compare the theoretical energy input required by two different cooking devices to deliver the same amount of useful energy. This is a ‘conservation of useful energy’ assumption. If the useful energy delivered by both devices is the same, then:
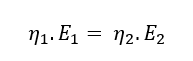
Then an energy ratio (based on efficiencies) for comparing the consumption of any two fuels can be expressed as:
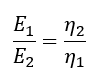
where E1 and η1 are the gross fuel energy input and conversion efficiency of device 1, and E2 and η2 are the gross fuel energy input and conversion efficiency of a second device.
There is a wide body of literature on the efficiency of stoves, particularly improved biomass stoves and there is a correspondingly wide range of efficiency figures published. However, for the purposes of the paper, we used generic efficiency values for traditional charcoal stoves given in the UNFCCC Clean Development Mechanism Default values for common parameters1. Efficiency values for gas and electric devices were drawn from the US Department of Energy test procedures for conventional cooking products2:
- Default value for a pre-project device using charcoal — 25%;
- Mean efficiency for gas stove (LPG) — 44%;
- Mean efficiency for electric coil hotplate — 72%;
- Mean efficiency for electric induction stove — 73%.
There are multiple standards for testing, including the US DOE and the Water Boiling Test, and so you can find a range of efficiency figures for modern cooking devices (gas and electric), and the figures above will be subject to dispute and debate. For example, induction stoves are widely regarded as being more efficient than hotplates but, whilst this may be true in general practice, studies have shown that the difference can be minimal if the right size of pots is used, but that’s another argument. Although subject to some variation, we felt that it is safe enough to use these standard reference values in the study.
These values give energy ratios based on efficiencies for charcoal to electricity of 2.9, and 1.8 for charcoal to LPG. However, when we look at the real life empirical data, we get significantly higher ratios; remember, these observations are based on hundreds of measured cooking events across multiple countries.
The ratios from empirical data seem to depend on the style of cooking, so the paper points out that energy consumption figures tend to be higher for African cooking than for Asian cooking. Asian cooking tends to be quicker than the ‘long’ cook dishes typical of African diets.
The real life, empirical data gives charcoal to electricity energy ratios for Africa ranging from 11 (hotplate) to 14 (induction). Energy ratios for Asia tends to be lower, ranging from 6 to 7 for hotplates and induction respectively. All of these actual measured values are much higher than the energy ratios based on the method described above using efficiencies and assuming a conservation of useful energy. The difference is not insubstantial, as ratios from empirical data are a factor of two to four times higher than those based on efficiencies. One gets a similar effect with LPG. LPG to electricity energy ratios calculated from empirical data are approximately 3 in Africa and 2.5 in Asia; these values are also higher than the energy ratios based on efficiencies (using conservation of useful energy) but closer, with a factor just less than two.
| Stove Combinations | Reference Estimates* | Results (from paper) Africa | Results (from paper) Asia |
|---|---|---|---|
| Charcoal/hotplate | 2.9 | 10.9 | 6 |
| Charcoal/induction | 2.9 | 14.1 | 7.3 |
| LPG/hotplate | 1.6 | 2.7 | 2.2 |
| LPG/induction | 1.7 | 3.5 | 2.6 |
| Charcoal/LPG | 1.8 | 4.1 | 2.8 |

So why are the calculated values based on efficiencies so different from the measured empirical values?
We think that it comes down to the difference between laboratory or test conditions used to measure stove efficiencies, and real life behaviour in households kitchens across Africa and Asia. This doesn’t mean that test efficiency figures are wrong , it’s just that the test protocols don’t reflect the way cooks behave in practice. There is no reason to believe that the thermal conversion efficiencies of stoves as used in a kitchen deviate substantially from efficiencies as measured in a lab, rather the amount of energy used also depends on the behaviour of the cook. Hager and Morawicki3 give a great summary of ways in which the behaviour of the cook can affect energy consumption:
- “Patient” vs. “hurried” cooks — hurried cooks who do not bother to control the stove use twice as much energy. We highlighted the importance of this in an earlier blog.
- Simmering vs. boiling — controlling heat input to achieve a simmer can save over 70%.
- Putting a lid on the pot reduces latent heat of evaporation losses.
- How much of the pot capacity is used — a pot filled to 20% capacity uses twice as much energy as a full pot.
- Passive cooking — partly cooking a dish, then allowing cooking to complete as it cools down.
- Flat pots — using pots that have not been damaged can save over 40%.
- Soaking dried foods, e.g., beans — can save up to 20%.
In contrast, tests to determine the efficiencies of cooking devices are highly prescriptive, designed to be as repeatable as possible. They also follow cooking practices leading to optimal energy use so, for example, the technician will make sure that the lid is always on, the fuel is extinguished as soon as the food is cooked, a good quality pot is used, and so on. But that’s not what actually happens in real world kitchens. When you leave cooking to a real, busy , distracted person working in a real kitchen, their cooking behaviour deviates from optimal, and additional energy losses from the poor cooking practices listed above creep in.
The extra energy consumption that results from these behaviours cannot be regarded as ‘useful’ energy, even if it is transferred to the pot, as it is not necessary for the successful cooking of the food and hence represents unnecessary losses. Therefore, the empirical data shows that the conservation of useful energy assumption does not hold.
All of these poor practices can take place when cooking with any fuel, but different technology and fuel combinations can minimise the scope for these behavioural energy losses. One of the most important features of any cooking device is its control. For example, the power of a charcoal stove cannot be controlled easily or quickly – okay, it can to a certain extent, but it requires a lot of skill on the part of the cook. In contrast, LPG and electric stoves can easily be controlled by the touch of a button or the turn of a knob. A charcoal stove also needs to be lit before it is needed for cooking in order to get the coals up to temperature. A skilled cook can judge the lighting time so that the stove is at temperature just when it is needed – but this is a skill. Energy released during this heating up period is not utilised – leading to increases losses. Energy can also be lost when charcoal cools down after cooking. In contrast, LPG and electricity can be turned on and off just when they are needed. These are just two examples of controllability that help explain why the amount of charcoal used in everyday cooking tends to be much more than the theoretical requirement, whereas the amount of LPG used can be closer to the theoretical amount, calculated from efficiency values.
This difference between energy ratios calculated using stove efficiencies with conservation of useful energy and real life measured empirical energy ratios has important implications for any work that relies on comparing the energy consumed or the cost of cooking with different fuels. The calculation of emissions reductions for carbon credits is an example of the former, and clean cooking policies and strategies are examples of the latter. Empirical energy ratios have already been incorporated into the workings of Gold Standard’s “Methodology for metered & measured energy cooking devices”. This approach has also been brought forward into alternative methodologies, and is included in the draft Comprehensive Lowered Emission Assessment and Reporting (CLEAR) Methodology currently under development by the Clean Cooking and Climate Consortium.
The difference between calculated and measured energy ratios also challenges some of the recent modelling of cost of cooking. Many studies modelling the cost of cooking start with data on the energy needed to cook with a given fuel, and then estimate the energy needed to meet the same cooking load with alternative fuels. For example, Nerini et al. estimated the net energy required to cook a meal in Kenya (the useful energy into the pot) from observations of households using improved charcoal stoves4. The equivalent amount of alternative fuels was then calculated by dividing the useful energy figure by estimated efficiencies for alternative stoves. This is also the approach used by sophisticated models such as OSeMOSYS and OnSTOVE, which optimise fuel choices on the basis of fuel cost (along with other factors). This work on empirical energy ratios suggests that where such modelling relies on stove efficiencies, it may be underestimating the role to be played in least cost scenarios by modern cooking fuels. Clearly, this is an issue that needs addressing, and is an area that MECS and the CCG programme are beginning to explore together.
As we move forward and partner with sophisticated modelling and integrated energy planning initiatives, it will be important to develop more realistic methods for comparing the energy and costs associated with different cooking fuels that are based on emerging real life data, such as that discussed above. As clean cooking gains more attention globally, all sorts of people who may not necessarily be experts in cooking will get involved, which is great, but they need to understand that cooking is not as simple as switching on a light bulb – you’ve got to take into account the behaviour of the cook.
…………………………………………
[1] https://cdm.unfccc.int/methodologies/PAmethodologies/tools/am-tool-33-v2.0.pdf
[2] https://public-inspection.federalregister.gov/2014-28212.pdf?1417528066
[3] Hager, T. J., & Morawicki, R. (2013). Energy consumption during cooking in the residential sector of developed nations: A review. Food Policy, 40, 54–63. https://doi.org/10.1016/j.foodpol.2013.02.003
[4] Nerini, F. F., Ray, C., & Boulkaid, Y. (2017). The cost of cooking a meal. the case of Nyeri County, Kenya. Environmental Research Letters, 12(6). https://doi.org/10.1088/1748-9326/aa6fd0
Figure 1 (featured image, top): Cooking on an induction hob (photo credit: ATEC copyright).